Pues resulta que mi Sobrino me ha pedido ayuda con Árboles y Grafos, pero ha esperado al último momento y no me va a ser posible dedicarle un rato. Así que aprovecho para publicar esta entrada y, con suerte, puede ayudarle.

Temo que esta entrada será un glosario de conceptos, aunque pueden venirnos bien para repasar

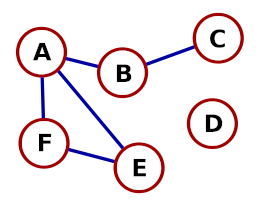
Conceptos generales

Un nodo es un elemento de un Árbol o un Grafo.

Un arco o arista es algo puramente conceptual: consiste en un “enlace” entre dos nodos. Es decir: es una relación entre los dos nodos.

Si esta relación se aplica en un único sentido, como por ejemplo, si establecemos la relación “es padre de”, entonces tendremos un arco dirigido.

Y ahora que sabemos tantas cosas, vamos por la chicha :D

Árboles

Es una estructura jerárquica, en la que sólo hay un nodo que no tiene padre, llamado raíz y el resto tiene, exactamente, un único padre.

Se pueden distinguir los nodos hoja, que no son más que nodos que no tienen hijos, es decir, son terminales.

En un árbol, todos los arcos son dirigidos, ya que siempre implican una relación “es padre de”.

Imagináos un árbol de directorios: los directorios y ficheros como tales son nodos; los ficheros son nodos hoja. El directorio “/” en GNU/Linux y “c:\” en Windows serían los nodos raíz en cada uno de estos sistemas.

Y con esto sólo nos queda decir que el alto de un árbol consiste en contar el número de hijos de la rama más larga.

Como la gente se aburre mucho, hay mogollón de categorías de árboles.

Árboles binarios

Es un árbol en el que cada uno de sus nodos puede tener entre 0 y 2 hijos.

Ahora mismo no se me ocurre una utilidad, pero es el resultado de aplicar el típico sistema de adivinación, en el que te van haciendo preguntas de tipo “sí/no” hasta que llegan a un nodo que no tiene hijos, momento en el que te adivinan lo que estabas pensando.

Árboles balanceados

Son árboles binarios, donde cualquier rama que elijamos tendrá una longitud igual a la altura del árbol o la altura del árbol menos 1. Vamos, que si te imaginas los nodos como una balanza, cojas el nodo que cojas, cada lado pesará más o menos lo mismo (ojo al “cojas el nodo que cojas”, ya que se puede ver cada nodo como la raíz de un sub-árbol, y todos deben estar balanceados).

Árboles n-arios

Como la propia palabra indica, es un árbol con un número variable de hijos.

Si tenemos un único nodo con 3 hijos, todo el árbol será n-ario. Dicho de otra manera: si no es binario, es n-ario.

Recorriendo el árbol

Si construimos un árbol es porque, tarde o temprano, lo recorreremos. Así que podemos hacerlo de dos maneras:

• En anchura, si miramos primero el contenido de los hermanos.
• En altura, si miramos primero el contenido de los hijos.

Programáticamente, la diferencia es el orden de dos llamadas a función (poco más o menos). En cuanto a la eficiencia… depende de lo que estemos haciendo.

Imagináos que metemos todas las palabras del diccionario en un árbol. En el primer nivel tendremos un nodo raíz vacío, que tendrá como hijos a todas las letras. Después, cada letra se relacionará con otras letras de manera que si lo recorremos en altura tendremos una palabra. ¿Ya os lo imagináis? Pues ahora queremos saber cuántas palabras tienen un mismo prefijo (al prefijo se le suele llamar raíz, pero para no confundir con los árboles, le llamaremos prefijo). Para ello, tendremos que recorrer el árbol en altura, seleccionando los hijos de acuerdo a las letras que encontremos, y devolver el número de hijos del último nodo.

Usos

En informática, el uso de los árboles es muy importante:

• Los sistemas de ficheros son árboles.
• Los archivos XML son árboles. Un archivo HTML también es un árbol.
• Un sistema de tablas Hash genera un árbol si tiene varios niveles.
• En general, cualquier sistema jerárquico suele ser un árbol.

Grafos

Un grafo consiste en un conjunto de nodos unidos por arcos.

No hay más reglas. Eso significa que se nos pueden dar ciertas situaciones, como encontrarnos islas, si tenemos dos grafos en los que ninguno de sus nodos se relacionan con los nodos del otro grafo. También podemos tener ciclos si, siguiendo las relaciones de un nodo a otro podemos volver al nodo inicial.

Diremos que es un grafo dirigido si todos sus arcos son arcos dirigidos.

Un término divertido es el de camino Euleriano, que es un camino que permite recorrer todos los arcos del grafo sin pasar dos veces por el mismo y volviendo de nuevo al nodo original. El nombre raro viene de la desgracia de que Euler les pusiera el nombrecito :D

Existen ocasiones en la que interesa que los arcos dejen de ser conceptuales y tengan un valor. Este valor, a menudo, se denomina peso o coste, y es de suma importancia.

Y ahora que ya he soltado toda esta basura… ¿Qué es un grafo de verdad?

Fijaos en un plano de vuestra ciudad. Eso es un grafo. Cada calle es un arco o arista y cada cruce, un nodo.

¿Y un grafo dirigido? Ahora nos fijamos en el plano de vuestra ciudad, pero como si fuéramos un coche. Hay calles que sólo se pueden recorrer en un sentido.

¿Y el peso o coste? Cuando vais a casa de vuestros amigos no elegís un camino al azar: tratáis de buscar el camino más corto. ¿Cómo lo elegís? Porque cada calle (arco) os lleva un tiempo que, en este caso, es su coste.

Habrá ocasiones, como en el plano, en las que nos interese minimizar el coste, mientras que en otras lo llamaremos beneficio y nos interesará maximizarlo. Por ejemplo, una empresa de transportes verá como beneficio el número de paquetes que puede entregar siguiendo un camino determinado. O el comecocos verá como beneficio cuántas bolitas puede comerse sin que le pille un fantasma :D

Tan solo me queda deciros que las islas o sub-grafos aislados no suelen ser deseables en la informática habitual, ya que te pueden colgar el sistema.

Referencias

Pues, en esta ocasión, he tirado de memoria. Probablemente se me hayan olvidado cosas, así que estoy abierto a lo que queráis preguntar.